Vi fortsätter att hantera vektorer. Vid första lektionen Vektorer för dummies Vi tittade på begreppet vektor, handlingar med vektorer, vektorkoordinater och de enklaste problemen med vektorer. Om du kom till denna sida för första gången från en sökmotor rekommenderar jag starkt att du läser ovanstående introduktionsartikel, eftersom du för att behärska materialet behöver vara bekant med de termer och notationer jag använder, ha grundläggande kunskaper om vektorer och kunna lösa grundläggande problem. Den här lektionen är en logisk fortsättning på ämnet, och i den kommer jag att analysera i detalj typiska uppgifter som använder den skalära produkten av vektorer. Detta är en MYCKET VIKTIG aktivitet.. Försök att inte hoppa över exemplen; de kommer med en användbar bonus - övning hjälper dig att konsolidera materialet du har täckt och bli bättre på att lösa vanliga problem inom analytisk geometri.
Addition av vektorer, multiplikation av en vektor med ett tal.... Det vore naivt att tro att matematiker inte har kommit på något annat. Utöver de åtgärder som redan diskuterats finns det ett antal andra operationer med vektorer, nämligen: prickprodukt av vektorer, vektorprodukt av vektorer Och blandad produkt av vektorer. Den skalära produkten av vektorer är bekant för oss från skolan; de andra två produkterna hör traditionellt till den högre matematikens kurs. Ämnena är enkla, algoritmen för att lösa många problem är enkel och begriplig. Den enda saken. Det finns en anständig mängd information, så det är inte önskvärt att försöka bemästra och lösa ALLT PÅ EN GÅNG. Detta gäller särskilt för dummies, tro mig, författaren vill absolut inte känna sig som Chikatilo från matematiken. Tja, inte från matematiken, förstås, heller =) Mer förberedda elever kan använda material selektivt, i en viss mening, "få" den saknade kunskapen, för dig kommer jag att vara en ofarlig greve Dracula =)
Låt oss äntligen öppna dörren och se med entusiasm vad som händer när två vektorer möter varandra...
Först om vinkel mellan vektorer. Jag tror att alla intuitivt förstår vad vinkeln mellan vektorer är, men för säkerhets skull, lite mer detaljer. Låt oss överväga fria vektorer som inte är noll och . Om du plottar dessa vektorer från en godtycklig punkt kommer du att få en bild som många redan har föreställt sig mentalt: 
Jag erkänner, här beskrev jag situationen endast på nivån av förståelse. Om du behöver en strikt definition av vinkeln mellan vektorer, se läroboken för praktiska problem, i princip är det ingen nytta för oss. Även HÄR OCH HÄR kommer jag att ignorera nollvektorer på ställen på grund av deras låga praktiska betydelse. Jag gjorde en reservation specifikt för avancerade webbplatsbesökare som kan förebrå mig för den teoretiska ofullständigheten i några efterföljande uttalanden.
kan ta värden från 0 till 180 grader (0 till radianer), inklusive. Analytiskt skrivs detta faktum i form av en dubbel ojämlikhet:
eller 
(i radianer). I litteraturen är vinkelsymbolen ofta överhoppad och enkel skriven.
Definition: Den skalära produkten av två vektorer är ett TAL lika med produkten av längderna av dessa vektorer och cosinus för vinkeln mellan dem: 
Nu är detta en ganska strikt definition.
Vi fokuserar på viktig information:
Beteckning: den skalära produkten betecknas med eller helt enkelt.
Resultatet av operationen är ett NUMMER: Vektor multipliceras med vektor, och resultatet är ett tal. Faktum är att om längderna på vektorer är tal, är cosinus för en vinkel ett tal, då deras produkt 
kommer också att vara ett nummer.
Bara ett par uppvärmningsexempel:
Exempel 1
Lösning: Vi använder formeln 
. I detta fall:
Svar:
Cosinusvärden finns i trigonometrisk tabell. Jag rekommenderar att du skriver ut det - det kommer att behövas i nästan alla delar av tornet och kommer att behövas många gånger.
Ur en rent matematisk synvinkel är den skalära produkten dimensionslös, det vill säga resultatet, i det här fallet, är bara en siffra och det är det. Ur fysikproblemens synvinkel har en skalär produkt alltid en viss fysisk betydelse, det vill säga efter resultatet måste en eller annan fysisk enhet anges. Ett kanoniskt exempel på att beräkna en krafts arbete kan hittas i vilken lärobok som helst (formeln är exakt en skalär produkt). En krafts arbete mäts i Joule, därför kommer svaret att skrivas ganska specifikt, till exempel .
Exempel 2
Hitta om 
, och vinkeln mellan vektorerna är lika med .
Detta är ett exempel för dig att lösa på egen hand, svaret finns i slutet av lektionen.
I exempel 1 visade sig den skalära produkten vara positiv och i exempel 2 visade den sig vara negativ. Låt oss ta reda på vad tecknet på den skalära produkten beror på. Låt oss titta på vår formel: 
. Längden på vektorer som inte är noll är alltid positiva: , så tecknet kan bara bero på värdet av cosinus.
Notera: För att bättre förstå informationen nedan är det bättre att studera cosinusgrafen i manualen Funktionsdiagram och egenskaper. Se hur cosinusen beter sig på segmentet.
Som redan noterats kan vinkeln mellan vektorerna variera inom 
, och följande fall är möjliga:
1) Om hörn mellan vektorer kryddad: 
(från 0 till 90 grader), sedan 
, Och punktprodukten kommer att vara positiv samregisserad, då anses vinkeln mellan dem vara noll, och den skalära produkten kommer också att vara positiv. Eftersom formeln förenklar: .
2) Om hörn mellan vektorer trubbig: 
(från 90 till 180 grader), då 
, och på motsvarande sätt, prickprodukten är negativ: . Specialfall: om vektorerna motsatta riktningar, då beaktas vinkeln mellan dem expanderat: (180 grader). Den skalära produkten är också negativ, eftersom
De omvända påståendena är också sanna:
1) Om , då är vinkeln mellan dessa vektorer spetsig. Alternativt är vektorerna samriktade.
2) Om , då är vinkeln mellan dessa vektorer trubbig. Alternativt är vektorerna i motsatta riktningar.
Men det tredje fallet är av särskilt intresse:
3) Om hörn mellan vektorer hetero: (90 grader), sedan skalär produkt är noll: . Det omvända är också sant: om , då . Uttalandet kan formuleras kompakt enligt följande: Den skalära produkten av två vektorer är noll om och endast om vektorerna är ortogonala. Kort matematisk notation: 
! Notera
: Låt oss upprepa grunderna i matematisk logik: En dubbelsidig logisk konsekvensikon läses vanligtvis "om och bara om", "om och endast om". Som du kan se är pilarna riktade i båda riktningarna - "från detta följer detta, och vice versa - från det följer detta." Vad är förresten skillnaden från envägsföljningsikonen? Ikonen anger bara det, att "av detta följer detta", och det är inte ett faktum att motsatsen är sann. Till exempel: , men inte alla djur är en panter, så i det här fallet kan du inte använda ikonen. Samtidigt, istället för ikonen Burk använd ensidig ikon. Till exempel, när vi löste problemet, fick vi reda på att vi drog slutsatsen att vektorerna är ortogonala: 
- en sådan post kommer att vara korrekt och till och med lämpligare än 
.
Det tredje fallet har stor praktisk betydelse, eftersom det låter dig kontrollera om vektorer är ortogonala eller inte. Vi kommer att lösa detta problem i den andra delen av lektionen.
Låt oss återgå till situationen när två vektorer samregisserad. I det här fallet är vinkeln mellan dem noll, , och den skalära produktformeln har formen: .
Vad händer om en vektor multipliceras med sig själv? Det är tydligt att vektorn är justerad med sig själv, så vi använder ovanstående förenklade formel:
Numret är uppringt skalär kvadrat vektor och betecknas som .
Således, den skalära kvadraten av en vektor är lika med kvadraten på längden på den givna vektorn:
Från denna likhet kan vi få en formel för att beräkna längden på vektorn:
Än så länge verkar det oklart, men målen för lektionen kommer att sätta allt på sin plats. För att lösa problemen behöver vi också egenskaper hos punktprodukten.
För godtyckliga vektorer och valfritt tal är följande egenskaper sanna:
1) – kommutativ eller kommutativ skalär produktlag.
2) 
– distribution eller distributiv skalär produktlag. Helt enkelt kan du öppna fästena.
3) 
– associativ eller associativ skalär produktlag. Konstanten kan härledas från den skalära produkten.
Ofta upplevs alla möjliga egenskaper (som också behöver bevisas!) av eleverna som onödigt skräp, som bara behöver memoreras och säkert glömmas bort direkt efter tentamen. Det verkar som om det som är viktigt här, alla vet redan från första klass att omorganisering av faktorerna inte förändrar produkten: . Jag måste varna dig för att i högre matematik är det lätt att röra till saker med ett sådant tillvägagångssätt. Så, till exempel, är den kommutativa egenskapen inte sann för algebraiska matriser. Det är inte heller sant för vektorprodukt av vektorer. Därför är det åtminstone bättre att fördjupa sig i alla egenskaper som du stöter på i en högre matematikkurs för att förstå vad som kan göras och vad som inte kan göras.
Exempel 3
.
Lösning: Låt oss först klargöra situationen med vektorn. Vad är det här egentligen? Summan av vektorer är en väldefinierad vektor, som betecknas med . En geometrisk tolkning av handlingar med vektorer finns i artikeln Vektorer för dummies. Samma persilja med en vektor är summan av vektorerna och .
Så, enligt tillståndet, krävs det att hitta den skalära produkten. I teorin måste du tillämpa arbetsformeln 
, men problemet är att vi inte vet längden på vektorerna och vinkeln mellan dem. Men villkoret ger liknande parametrar för vektorer, så vi tar en annan väg:
(1) Ersätt uttrycken för vektorerna.
(2) Vi öppnar parentesen enligt regeln för multiplicering av polynom en vulgär tungvridare kan hittas i artikeln Komplexa tal eller Integrering av en bråk-rationell funktion. Jag kommer inte att upprepa mig själv =) Förresten, den distribuerande egenskapen hos den skalära produkten tillåter oss att öppna fästena. Vi har rätten.
(3) I de första och sista termerna skriver vi kompakt de skalära kvadraterna av vektorerna: 
. I den andra termen använder vi den skalära produktens commuterbarhet: .
(4) Vi presenterar liknande termer: .
(5) I den första termen använder vi den skalära kvadratformeln, som nämndes för inte så länge sedan. Under den sista terminen fungerar alltså samma sak: . Vi utökar den andra termen enligt standardformeln 
.
(6) Ersätt dessa villkor 
, och utför noggrant de slutliga beräkningarna.
Svar:
Ett negativt värde på den skalära produkten anger att vinkeln mellan vektorerna är trubbig.
Problemet är typiskt, här är ett exempel för att lösa det själv:
Exempel 4
Hitta skalärprodukten av vektorer och om det är känt att 
.
Nu en annan vanlig uppgift, bara för den nya formeln för längden på en vektor. Notationen här kommer att vara lite överlappande, så för tydlighetens skull skriver jag om den med en annan bokstav:
Exempel 5
Hitta längden på vektorn if 
.
Lösning blir som följer:
(1) Vi tillhandahåller uttrycket för vektorn.
(2) Vi använder längdformeln: , medan hela uttrycket ve fungerar som vektorn "ve".
(3) Vi använder skolans formel för kvadraten på summan. Lägg märke till hur det fungerar konstigt här: – det är faktiskt kvadraten på skillnaden, och det är faktiskt så det är. De som vill kan ordna om vektorerna: - samma sak händer, fram till omarrangemanget av termerna.
(4) Det som följer är redan bekant från de två tidigare problemen.
Svar: 
Eftersom vi pratar om längd, glöm inte att ange dimensionen - "enheter".
Exempel 6
Hitta längden på vektorn if 
.
Detta är ett exempel för dig att lösa på egen hand. Fullständig lösning och svar i slutet av lektionen.
Vi fortsätter att pressa ut användbara saker ur prickprodukten. Låt oss titta på vår formel igen 
. Med hjälp av proportionsregeln återställer vi vektorernas längder till nämnaren på vänster sida: 
Låt oss byta delar: 
Vad är meningen med denna formel? Om längden på två vektorer och deras skalära produkt är kända, kan cosinus för vinkeln mellan dessa vektorer, och följaktligen själva vinkeln, beräknas.
Är en punktprodukt ett nummer? Siffra. Är vektorlängder tal? Tal. Det betyder att ett bråk också är ett tal. Och om cosinus för vinkeln är känd: 
, sedan med den inversa funktionen är det lätt att hitta själva vinkeln: 
.
Exempel 7
Hitta vinkeln mellan vektorerna och om det är känt att .
Lösning: Vi använder formeln:
I slutskedet av beräkningarna användes en teknisk teknik - eliminera irrationalitet i nämnaren. För att eliminera irrationalitet multiplicerade jag täljaren och nämnaren med .
Så om 
, Den där: 
Värdena för inversa trigonometriska funktioner kan hittas av trigonometrisk tabell. Även om detta händer sällan. I problem med analytisk geometri, mycket oftare en klumpig björn som , och värdet på vinkeln måste hittas ungefär med hjälp av en miniräknare. Egentligen kommer vi att se en sådan bild mer än en gång.
Svar: 
Återigen, glöm inte att ange dimensionerna - radianer och grader. Personligen, för att uppenbarligen "lösa alla frågor", föredrar jag att ange båda (såvida inte villkoret naturligtvis kräver att svaret endast presenteras i radianer eller endast i grader).
Nu kan du självständigt hantera en mer komplex uppgift:
Exempel 7*
Angivna är vektorernas längder och vinkeln mellan dem. Hitta vinkeln mellan vektorerna , .
Uppgiften är inte så svår som den är i flera steg.
Låt oss titta på lösningsalgoritmen:
1) Enligt villkoret måste du hitta vinkeln mellan vektorerna och , så du måste använda formeln 
.
2) Hitta den skalära produkten (se exempel nr 3, 4).
3) Hitta längden på vektorn och längden på vektorn (se exempel nr 5, 6).
4) Slutet på lösningen sammanfaller med exempel nr 7 - vi känner till talet , vilket betyder att det är lätt att hitta själva vinkeln: 
En kort lösning och svar i slutet av lektionen.
Den andra delen av lektionen ägnas åt samma skalära produkt. Koordinater. Det blir ännu lättare än i första delen.
Svar:
Det behöver inte sägas att det är mycket trevligare att hantera koordinater.
Exempel 14
Hitta skalärprodukten av vektorer och om
Detta är ett exempel för dig att lösa på egen hand. Här kan du använda operationens associativitet, det vill säga inte räkna utan omedelbart ta trippeln utanför den skalära produkten och multiplicera den med den sist. Lösningen och svaret finns i slutet av lektionen.
I slutet av stycket, ett provokativt exempel på att beräkna längden på en vektor:
Exempel 15
Hitta längden på vektorer 
, Om
Lösning: Metoden från föregående avsnitt föreslår sig själv igen: men det finns ett annat sätt:
Låt oss hitta vektorn:
Och dess längd enligt den triviala formeln 
:
Prickprodukten är inte aktuell här alls!
Det är inte heller användbart när man beräknar längden på en vektor:
Sluta. Borde vi inte dra nytta av den uppenbara egenskapen vektorlängd? Vad kan du säga om vektorns längd? Denna vektor är 5 gånger längre än vektorn. Riktningen är motsatt, men det spelar ingen roll, eftersom vi pratar om längd. Uppenbarligen är vektorns längd lika med produkten modul antal per vektorlängd:
– modultecknet ”äter” talets möjliga minus.
Således:
Svar:
Nu har vi fullständig information för att använda den tidigare härledda formeln för cosinus för vinkeln mellan vektorer 
uttrycka genom vektorkoordinater:
Cosinus för vinkeln mellan planvektorer och, specificerat på ortonormal basis, uttrycks med formeln:
.
Cosinus för vinkeln mellan rymdvektorer, specificerad på ortonormal basis, uttrycks med formeln: 
Exempel 16
Givet tre hörn i en triangel. Hitta (vertexvinkel).
Lösning: Enligt villkoren krävs inte ritningen, men ändå: 
Den önskade vinkeln är markerad med en grön båge. Låt oss omedelbart komma ihåg skolbeteckningen för en vinkel: – särskild uppmärksamhet på genomsnitt bokstav - detta är spetsen på vinkeln vi behöver. För korthetens skull kan du också skriva helt enkelt .
Från ritningen är det ganska uppenbart att triangelns vinkel sammanfaller med vinkeln mellan vektorerna och med andra ord: 
.
Det är tillrådligt att lära sig hur man utför analysen mentalt.
Låt oss hitta vektorerna: 
Låt oss beräkna den skalära produkten:
Och längden på vektorerna: 
Vinkelkosinus:
Detta är exakt ordningen för att slutföra uppgiften som jag rekommenderar för dummies. Mer avancerade läsare kan skriva beräkningarna "på en rad": 
Här är ett exempel på ett "dåligt" cosinusvärde. Det resulterande värdet är inte slutgiltigt, så det finns ingen mening med att bli av med irrationalitet i nämnaren.
Låt oss hitta själva vinkeln:
Om du tittar på ritningen är resultatet ganska troligt. För att kontrollera kan vinkeln även mätas med en gradskiva. Skada inte bildskärmslocket =)
Svar: 
I svaret glömmer vi inte det frågade om vinkeln på en triangel(och inte om vinkeln mellan vektorerna), glöm inte att ange det exakta svaret: och det ungefärliga värdet på vinkeln: 
, hittas med hjälp av en miniräknare.
De som har njutit av processen kan beräkna vinklarna och verifiera giltigheten av den kanoniska jämlikheten
Exempel 17
En triangel definieras i rymden av koordinaterna för dess hörn. Hitta vinkeln mellan sidorna och
Detta är ett exempel för dig att lösa på egen hand. Fullständig lösning och svar i slutet av lektionen
Ett kort sista avsnitt kommer att ägnas åt projektioner, som också involverar en skalär produkt:
Tänk på vektorerna och: 
Låt oss projicera vektorn på vektorn för att göra detta, från början och slutet av vektorn som vi utelämnar vinkelräta till vektor (gröna prickade linjer). Föreställ dig att ljusstrålar faller vinkelrätt på vektorn. Då kommer segmentet (röd linje) att vara vektorns "skugga". I detta fall är projektionen av vektorn på vektorn LÄNGDEN av segmentet. Det vill säga, PROJEKTION ÄR ETT TAL.
Detta NUMMER betecknas enligt följande: , "stor vektor" betecknar vektorn SOM projekt, "liten nedsänkt vektor" betecknar vektorn PÅ som projiceras.
Själva posten lyder så här: "projektion av vektor "a" på vektor "be".
Vad händer om vektorn "be" är "för kort"? Vi ritar en rak linje som innehåller vektorn "be". Och vektor "a" kommer redan att projiceras till vektorns riktning "vara", helt enkelt - till den raka linjen som innehåller vektorn "be". Samma sak kommer att hända om vektorn "a" skjuts upp i det trettionde riket - den kommer fortfarande att projiceras lätt på den raka linjen som innehåller vektorn "be".
Om vinkeln mellan vektorer kryddad(som på bilden), alltså
Om vektorerna ortogonal, alltså (projektionen är en punkt vars dimensioner anses vara noll).
Om vinkeln mellan vektorer trubbig(i figuren, ordna om vektorpilen mentalt), sedan (samma längd, men taget med ett minustecken).
Låt oss plotta dessa vektorer från en punkt: 
Uppenbarligen, när en vektor rör sig, ändras inte dess projektion
I. Den skalära produkten försvinner om och endast om minst en av vektorerna är noll eller om vektorerna är vinkelräta. Faktum är att om eller , eller då .
Omvänt, om de multiplicerade vektorerna inte är noll, då på grund av villkoret
när det följer:
Eftersom nollvektorns riktning är osäker kan nollvektorn anses vara vinkelrät mot vilken vektor som helst. Därför kan den indikerade egenskapen hos den skalära produkten formuleras mer kortfattat: den skalära produkten försvinner om och endast om vektorerna är vinkelräta.
II. Den skalära produkten har den kommutativa egenskapen:
Denna egenskap följer direkt av definitionen:
eftersom olika beteckningar för samma vinkel.
III. Fördelningslagen är oerhört viktig. Dess tillämpning är lika stor som i vanlig aritmetik eller algebra, där den är formulerad enligt följande: för att multiplicera en summa måste du multiplicera varje term och lägga till de resulterande produkterna, d.v.s.
Uppenbarligen är multiplikationen av flervärdiga tal i aritmetik eller polynom i algebra baserad på denna egenskap av multiplikation.
Denna lag har samma grundläggande betydelse i vektoralgebra, eftersom vi utifrån den kan tillämpa den vanliga regeln för att multiplicera polynom på vektorer.
Låt oss bevisa att för alla tre vektorer A, B, C är följande likhet sann:
Enligt den andra definitionen av den skalära produkten, uttryckt med formeln, får vi:
När vi nu tillämpar egenskapen för 2 projektioner från § 5, finner vi:
Q.E.D.
IV. Den skalära produkten har egenskapen att kombineras med avseende på en numerisk faktor; denna egenskap uttrycks med följande formel:
det vill säga att multiplicera skalärprodukten av vektorer med ett tal räcker det att multiplicera en av faktorerna med detta tal.
Det kommer också att finnas problem för dig att lösa på egen hand, som du kan se svaren på.
Om i problemet både längden på vektorerna och vinkeln mellan dem presenteras "på ett silverfat", så ser tillståndet för problemet och dess lösning ut så här:
Exempel 1. Vektorer ges. Hitta skalärprodukten av vektorer om deras längder och vinkeln mellan dem representeras av följande värden:
En annan definition är också giltig, helt likvärdig med definition 1.
Definition 2. Den skalära produkten av vektorer är ett tal (skalär) lika med produkten av längden av en av dessa vektorer och projektionen av en annan vektor på axeln som bestäms av den första av dessa vektorer. Formel enligt definition 2:
Vi kommer att lösa problemet med denna formel efter nästa viktiga teoretiska punkt.
Samma antal kan erhållas om vektorerna som multipliceras får sina koordinater.
Definition 3. Punktprodukten av vektorer är ett tal lika med summan av de parvisa produkterna av deras motsvarande koordinater.
Om två vektorer och på planet definieras av deras två Kartesiska rektangulära koordinater
då är skalärprodukten av dessa vektorer lika med summan av parvisa produkter av deras motsvarande koordinater:
.
Exempel 2. Hitta det numeriska värdet för projektionen av vektorn på axeln parallell med vektorn.
Lösning. Vi hittar skalärprodukten av vektorer genom att addera de parvisa produkterna av deras koordinater:
Nu måste vi likställa den resulterande skalära produkten med produkten av vektorns längd och projektionen av vektorn på en axel parallell med vektorn (i enlighet med formeln).
Vi finner längden på vektorn som kvadratroten av summan av kvadraterna av dess koordinater:
.
Vi skapar en ekvation och löser den:
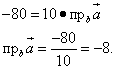
Svar. Det obligatoriska numeriska värdet är minus 8.
Om två vektorer och i rymden definieras av deras tre kartesiska rektangulära koordinater
,
då är den skalära produkten av dessa vektorer också lika med summan av parvisa produkter av deras motsvarande koordinater, bara det finns redan tre koordinater:
.
Uppgiften att hitta den skalära produkten med den övervägda metoden är efter att ha analyserat egenskaperna hos den skalära produkten. För i problemet måste du bestämma vilken vinkel de multiplicerade vektorerna bildar.
1. (kommutativ egenskap: omkastning av platserna för de multiplicerade vektorerna ändrar inte värdet på deras skalära produkt).
2. 
(associativ egenskap med avseende på en numerisk faktor: skalärprodukten av en vektor multiplicerad med en viss faktor och en annan vektor är lika med skalärprodukten av dessa vektorer multiplicerad med samma faktor).
3. 
(fördelningsegenskap i förhållande till summan av vektorer: skalärprodukten av summan av två vektorer av den tredje vektorn är lika med summan av skalärprodukterna av den första vektorn av den tredje vektorn och den andra vektorn av den tredje vektorn).
4. (skalär kvadrat av vektor större än noll), if är en vektor som inte är noll, och , if är en nollvektor.
I definitionerna av operationen som studeras har vi redan berört konceptet med en vinkel mellan två vektorer. Det är dags att förtydliga detta koncept.
I figuren ovan kan du se två vektorer som förs till ett gemensamt ursprung. Och det första du måste vara uppmärksam på är att det finns två vinklar mellan dessa vektorer - φ 1 Och φ 2 . Vilken av dessa vinklar förekommer i definitionerna och egenskaperna för skalärprodukten av vektorer? Summan av de betraktade vinklarna är 2 π och därför är cosinuserna för dessa vinklar lika. Definitionen av en punktprodukt inkluderar endast vinkelns cosinus och inte värdet av dess uttryck. Men egenskaperna tar bara hänsyn till en vinkel. Och detta är den av de två vinklarna som inte överstiger π , det vill säga 180 grader. I figuren anges denna vinkel som φ 1 .
1. Två vektorer kallas ortogonal Och vinkeln mellan dessa vektorer är rak (90 grader eller π /2), om skalärprodukten av dessa vektorer är noll :
.
Ortogonalitet i vektoralgebra är vinkelrätheten mellan två vektorer.
2. Två vektorer som inte är noll utgör vasst hörn (från 0 till 90 grader, eller, vilket är samma - mindre π prickprodukten är positiv .
3. Två vektorer som inte är noll utgör trubbig vinkel (från 90 till 180 grader, eller vad är samma sak - mer π /2) om och endast om de prickprodukten är negativ .
Exempel 3. Koordinaterna ges av vektorerna:
.
Beräkna skalärprodukterna för alla par av givna vektorer. Vilken vinkel (spets, höger, trubbig) bildar dessa vektorpar?
Lösning. Vi kommer att beräkna genom att lägga till produkterna av motsvarande koordinater.
Vi fick ett negativt tal, så vektorerna bildar en trubbig vinkel.
Vi fick ett positivt tal, så vektorerna bildar en spetsig vinkel.
Vi fick noll, så vektorerna bildar en rät vinkel.
Vi fick ett positivt tal, så vektorerna bildar en spetsig vinkel.
.
Vi fick ett positivt tal, så vektorerna bildar en spetsig vinkel.
För självtest kan du använda online-kalkylator Punktprodukt av vektorer och cosinus för vinkeln mellan dem.
Exempel 4. Givet längden på två vektorer och vinkeln mellan dem:
.
Bestäm vid vilket värde av talet vektorerna och är ortogonala (vinkelräta).
Lösning. Låt oss multiplicera vektorerna med hjälp av regeln för att multiplicera polynom:
Låt oss nu beräkna varje term:
.
Låt oss skapa en ekvation (produkten är lika med noll), lägg till liknande termer och lös ekvationen:
Svar: vi fick värdet λ = 1,8, där vektorerna är ortogonala.
Exempel 5. Bevisa att vektorn 
ortogonal (vinkelrätt) mot vektorn
Lösning. För att kontrollera ortogonalitet multiplicerar vi vektorerna och som polynom och ersätter istället uttrycket som ges i problemsatsen:
.
För att göra detta måste du multiplicera varje term (term) i det första polynomet med varje term i det andra och lägga till de resulterande produkterna:
.
I det resulterande resultatet reduceras fraktionen med. Följande resultat erhålls:
Slutsats: som ett resultat av multiplikation fick vi noll, därför är ortogonaliteten (vinkelräthet) av vektorerna bevisad.
Exempel 6. Längden på vektorerna och anges, och vinkeln mellan dessa vektorer är π /4 . Bestäm till vilket värde μ vektorer och är inbördes vinkelräta.
För självtest kan du använda online-kalkylator Punktprodukt av vektorer och cosinus för vinkeln mellan dem.
Ibland är det fördelaktigt för klarheten att representera två multiplicerade vektorer i form av matriser. Sedan representeras den första vektorn som en radmatris och den andra som en kolumnmatris:
Då blir den skalära produkten av vektorer produkten av dessa matriser :
Resultatet är detsamma som erhålls med metoden vi redan har övervägt. Vi fick ett enda tal, och produkten av en radmatris med en kolumnmatris är också ett enda tal.
Det är lämpligt att representera produkten av abstrakta n-dimensionella vektorer i matrisform. Således kommer produkten av två fyrdimensionella vektorer att vara produkten av en radmatris med fyra element med en kolumnmatris också med fyra element, produkten av två femdimensionella vektorer kommer att vara produkten av en radmatris med fem element av en kolumnmatris också med fem element, och så vidare.
Exempel 7. Hitta skalära produkter av par av vektorer
,
med hjälp av matrisrepresentation.
Lösning. Det första vektorparet. Vi representerar den första vektorn som en radmatris och den andra som en kolumnmatris. Vi finner skalärprodukten av dessa vektorer som produkten av en radmatris och en kolumnmatris:
Vi representerar på liknande sätt det andra paret och finner:
Som du kan se var resultaten desamma som för samma par från exempel 2.
Härledningen av formeln för cosinus för vinkeln mellan två vektorer är mycket vacker och koncis.
Att uttrycka prickprodukten av vektorer
(1)
i koordinatform hittar vi först skalärprodukten av enhetsvektorerna. Den skalära produkten av en vektor med sig själv per definition:
Det som står i formeln ovan betyder: skalärprodukten av en vektor med sig själv är lika med kvadraten på dess längd. Cosinus noll är lika med ett, så kvadraten på varje enhet blir lika med ett:
Sedan vektorer
är parvis vinkelräta, kommer de parvisa produkterna av enhetsvektorerna att vara lika med noll:
Låt oss nu utföra multiplikationen av vektorpolynom:
Vi ersätter värdena för motsvarande skalära produkter av enhetsvektorerna till höger sida av likheten:
Vi får formeln för cosinus för vinkeln mellan två vektorer:
Exempel 8. Tre poäng ges A(1;1;1), B(2;2;1), C(2;1;2).
Hitta vinkeln.
Lösning. Hitta koordinaterna för vektorerna:
,
.
Med hjälp av cosinusvinkelformeln får vi:
Därav, .
För självtest kan du använda online-kalkylator Punktprodukt av vektorer och cosinus för vinkeln mellan dem.
Exempel 9. Två vektorer ges
Hitta summan, skillnaden, längden, prickprodukten och vinkeln mellan dem.
