Макияж. Уход за волосами. Уход за кожей

Величину угла между двумя различными плоскостями можно определить для любого взаимного расположения плоскостей.

Тривиальный случай если плоскости параллельны. Тогда угол между ними считается равным нулю.

Нетривиальный случай если плоскости пересекаются. Этому случаю и посвящено дальнейшее обсуждение. Сначала нам понадобится понятие двугранного угла.

9.1 Двугранный угол

Двугранный угол это две полуплоскости с общей прямой (которая называется ребром двугранного угла). На рис. 50 изображён двугранный угол, образованный полуплоскостями и; ребром этого двугранного угла служит прямая a, общая для данных полуплоскостей.

Рис. 50. Двугранный угол

Двугранный угол можно измерять в градусах или радианах словом, ввести угловую величину двугранного угла. Делается это следующим образом.

На ребре двугранного угла, образованного полуплоскостями и, возьмём произвольную точку M. Проведём лучи MA и MB, лежащие соответственно в данных полуплоскостях и перпендикулярные ребру (рис. 51 ).

Рис. 51. Линейный угол двугранного угла

Полученный угол AMB это линейный угол двугранного угла. Угол " = \AMB как раз и является угловой величиной нашего двугранного угла.

Определение. Угловая величина двугранного угла это величина линейного угла данного двугранного угла.

Все линейные углы двугранного угла равны друг другу (ведь они получаются друг из друга параллельным сдвигом). Поэтому данное определение корректно: величина " не зависит от конкретного выбора точки M на ребре двугранного угла.

9.2 Определение угла между плоскостями

При пересечении двух плоскостей получаются четыре двугранных угла. Если все они имеют одинаковую величину (по 90), то плоскости называются перпендикулярными; угол между плоскостями тогда равен 90 .

Если не все двугранные углы одинаковы (то есть имеются два острых и два тупых), то углом между плоскостями называется величина острого двугранного угла (рис. 52 ).

Рис. 52. Угол между плоскостями

9.3 Примеры решения задач

Разберём три задачи. Первая простая, вторая и третья примерно на уровне C2 на ЕГЭ по математике.

Задача 1. Найдите угол между двумя гранями правильного тетраэдра.

Решение. Пусть ABCD правильный тетраэдр. Проведём медианы AM и DM соответствующих граней, а также высоту тетраэдра DH (рис. 53 ).

Рис. 53. К задаче 1

Будучи медианами, AM и DM являются также высотами равносторонних треугольников ABC и DBC. Поэтому угол " = \AMD есть линейный угол двугранного угла, образованного гранями ABC и DBC. Находим его из треугольника DHM:

Ответ: arccos 1 3 .

Задача 2. В правильной четырёхугольной пирамиде SABCD (с вершиной S) боковое ребро равно стороне основания. Точка K середина ребра SA. Найдите угол между плоскостями

Решение. Прямая BC параллельна AD и тем самым параллельна плоскости ADS. Поэтому плоскость KBC пересекает плоскость ADS по прямой KL, параллельной BC (рис. 54 ).

Рис. 54. К задаче 2

При этом KL будет также параллельна прямой AD; следовательно, KL средняя линия треугольника ADS, и точка L середина DS.

Проведём высоту пирамиды SO. Пусть N середина DO. Тогда LN средняя линия треугольника DOS, и потому LN k SO. Значит, LN перпендикуляр к плоскости ABC.

Из точки N опустим перпендикуляр NM на прямую BC. Прямая NM будет проекцией наклонной LM на плоскость ABC. Из теоремы о трёх перпендикулярах следует тогда, что LM также перпендикулярна BC.

Таким образом, угол " = \LMN является линейным углом двугранного угла, образованного полуплоскостями KBC и ABC. Будем искать этот угол из прямоугольного треугольника LMN.

Пусть ребро пирамиды равно a. Сначала находим высоту пирамиды:

Решение. Пусть L точка пересечения прямых A1 K и AB. Тогда плоскость A1 KC пересекает плоскость ABC по прямой CL (рис.55 ).

A C

Рис. 55. К задаче 3

Треугольники A1 B1 K и KBL равны по катету и острому углу. Следовательно, равны и другие катеты: A1 B1 = BL.

Рассмотрим треугольник ACL. В нём BA = BC = BL. Угол CBL равен 120 ; стало быть, \BCL = 30 . Кроме того, \BCA = 60 . Поэтому \ACL = \BCA + \BCL = 90 .

Итак, LC ? AC. Но прямая AC служит проекцией прямой A1 C на плоскость ABC. По теореме о трёх перпендикулярах заключаем тогда, что LC ? A1 C.

Таким образом, угол A1 CA линейный угол двугранного угла, образованного полуплоскостями A1 KC и ABC. Это и есть искомый угол. Из равнобедренного прямоугольного треугольника A1 AC мы видим, что он равен 45 .

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

При решении геометрических задач в пространстве часто встречаются такие, где необходимо рассчитать углы между разными пространственными объектами. В данной статье рассмотрим вопрос нахождения углов между плоскостями и между ними и прямой.

Прямая в пространстве

Известно, что совершенно любая прямая на плоскости может быть определена следующим равенством:

Здесь a и b - некоторые числа. Если представить тем же самым выражением прямую в пространстве, то получится уже плоскость, параллельная оси z. Для математического определения пространственной прямой применяют иной способ решения, чем в двумерном случае. Он заключается в использовании понятия "направляющий вектор".

Примеры решения задач на определение угла пересечения плоскостей

Зная, как найти между плоскостями угол, решим следующую задачу. Даны две плоскости, уравнения которых имеют вид:

3 * x + 4 * y - z + 3 = 0;

X - 2 * y + 5 * z +1 = 0

Чему между плоскостями равен угол?

Чтобы ответить на вопрос задачи, вспомним, что коэффициенты, стоящие при переменных в уравнении плоскости общем, являются координатами вектора направляющего. Для указанных плоскостей имеем следующие координаты их нормалей:

n 1 ¯(3; 4; -1);

n 2 ¯(-1; -2; 5)

Теперь найдем произведение скалярное этих векторов и их модули, имеем:

(n 1 ¯ * n 2 ¯) = -3 -8 -5 = -16;

|n 1 ¯| = √(9 + 16 + 1) = √26;

|n 2 ¯| = √(1 + 4 + 25) = √30

Теперь можно подставить найденные числа в приведенную в предыдущем пункте формулу. Получаем:

α = arccos(|-16 | / (√26 * √30) ≈ 55,05 o

Полученное значение соответствует острому углу пересечения плоскостей, указанных в условии задачи.

Теперь рассмотрим другой пример. Даны две плоскости:

Пересекаются ли они? Выпишем значения координат их направляющих векторов, посчитаем скалярное произведение их и модули:

n 1 ¯(1; 1; 0);

n 2 ¯(3; 3; 0);

(n 1 ¯ * n 2 ¯) = 3 + 3 + 0 = 6;

|n 1 ¯| = √2;

|n 2 ¯| = √18

Тогда угол пересечения равен:

α = arccos(|6| / (√2 * √18) =0 o .

Этот угол говорит о том, что плоскости не пересекаются, а являются параллельными. Тот факт, что они не совпадают друг с другом проверить просто. Возьмем для этого произвольную точку, принадлежащую первой из них, например, P(0; 3; 2). Подставим ее координаты во второе уравнение, получим:

3 * 0 +3 * 3 + 8 = 17 ≠ 0

То есть точка P принадлежит только первой плоскости.

Таким образом, две плоскости параллельными являются, когда таковыми будут их нормали.

Плоскость и прямая

В случае рассмотрения взаимного расположения между плоскостью и прямой существует несколько больше вариантов, чем с двумя плоскостями. Связан этот факт с тем, что прямая является одномерным объектом. Прямая и плоскость могут быть:

• взаимно параллельными, в этом случае плоскость не пересекает прямую;
• последняя может принадлежать плоскости, при этом она также будет параллельна ей;
• оба объекта могут пересекаться под некоторым углом.

Рассмотрим сначала последний случай, поскольку он требует введения понятия об угле пересечения.

Прямая и плоскость, значение угла между ними

Если плоскость прямая пересекает, то она называется наклонной по отношению к ней. Точку пересечения принято называть основанием наклонной. Чтобы определить между этими геометрическими объектами угол, необходимо опустить из любой точки прямой перпендикуляр на плоскость. Тогда точка пересечения перпендикуляра с плоскостью и место пересечения с ней наклонной образуют прямую. Последняя называется проекцией исходной прямой на рассматриваемую плоскость. Острый и проекцией ее является искомым.

Несколько запутанное определение угла между плоскостью и наклонной прояснит рисунок ниже.

Здесь угол ABO - это угол между AB прямой и a плоскостью.

Чтобы записать формулу для него, рассмотрим пример. Пусть имеется прямая и плоскость, которые описываются уравнениями:

(x ; y ; z) = (x 0 ; y 0 ; z 0) + λ * (a; b; c);

A * x + B * x + C * x + D = 0

Рассчитать искомый угол для этих объектов можно легко, если найти скалярное произведение между направляющими векторами прямой и плоскости. Полученный острый угол следует вычесть из 90 o , тогда он получается между прямой и плоскостью.

Рисунок выше демонстрирует описанный алгоритм нахождения рассматриваемого угла. Здесь β - это угол между нормалью и прямой, а α - между прямой и ее проекцией на плоскость. Видно, что их сумма равна 90 o .

Выше была представлена формула, дающая ответ на вопрос, как между плоскостями найти угол. Теперь приведем соответствующее выражение для случая прямой и плоскости:

α = arcsin(|a * A + b * B + c * C| / (√(a 2 + b 2 + c 2) * √(A 2 + B 2 + C 2)))

Модуль в формуле позволяет вычислять только острые углы. Функция арксинуса появилась вместо арккосинуса благодаря использованию соответствующей формулы приведения между тригонометрическими функциями (cos(β) = sin(90 o-β) = sin(α)).

Задача: плоскость пересекает прямую

Теперь покажем, как работать с приведенной формулой. Решим задачу: необходимо вычислить угол между осью y и плоскостью, заданной уравнением:

Эта плоскость показана на рисунке.

Видно, что она пересекает оси y и z в точках (0; -12; 0) и (0; 0; 12) соответственно и параллельна оси x.

Направляющий вектор прямой y имеет координаты (0; 1; 0). Вектор, перпендикулярный заданной плоскости, характеризуется координатами (0; 1; -1). Применяем формулу для угла пересечения прямой и плоскости, получаем:

α = arcsin(|1| / (√1 * √2)) = arcsin(1 / √2) = 45 o

Задача: параллельная плоскости прямая

Теперь решим аналогичную предыдущей задачу, вопрос которой поставлен иначе. Известны уравнения плоскости и прямой:

x + y - z - 3 = 0;

(x; y; z) = (1; 0; 0) + λ * (0; 2; 2)

Необходимо выяснить, являются ли эти геометрические объекты параллельными друг другу.

Имеем два вектора: направляющий прямой равен (0; 2; 2) и направляющий плоскости равен (1; 1; -1). Находим их скалярное произведение:

0 * 1 + 1 * 2 - 1 * 2 = 0

Полученный ноль говорит о том, что угол между этими векторами равен 90 o , что доказывает прямой и плоскости параллельность.

Теперь проверим, является эта прямая только параллельной или же еще и лежит в плоскости. Для этого следует выбрать произвольную точку на прямой и проверить, принадлежит ли она плоскости. Например, примем λ = 0, тогда точка P(1; 0; 0) прямой принадлежит. Подставляем в уравнение плоскости P:

Точка P плоскости не принадлежит, а значит, и вся прямая в ней не лежит.

Где важно знать углы между рассмотренными геометрическими объектами?

Приведенные выше формулы и примеры решения задач представляют собой не только теоретический интерес. Они часто применяются для определения важных физических величин реальных объемных фигур, например призмы или пирамиды. Важно уметь определить между плоскостями угол при расчете объемов фигур и площадей их поверхностей. При этом, если в случае прямой призмы можно не использовать эти формулы для определения указанных величин, то для любого вида пирамиды их применение оказывается неизбежным.

Ниже рассмотрим пример использования изложенной теории для определения углов пирамиды с квадратным основанием.

Пирамида и ее углы

Ниже рисунок демонстрирует пирамиду, в основании которой лежит квадрат со стороной а. Высота фигуры составляет h. Нужно найти два угла:

• между боковой поверхностью и основанием;
• между боковым ребром и основанием.

Чтобы решить поставленную задачу, сначала следует ввести систему координат и определить параметры соответствующих вершин. На рисунке показано, что начало координат совпадает с точкой в центре квадратного основания. В этом случае плоскость основания описывается уравнением:

То есть для любых x и y значение третьей координаты всегда равно нулю. Боковая плоскость ABC пересекает ось z в точке B(0; 0; h), а ось y в точке с координатами (0; a/2; 0). Ось x она не пересекает. Это означает, что уравнение плоскости ABC можно записать в виде:

y / (a / 2) + z / h = 1 или

2 * h * y + a * z - a * h = 0

Вектор AB¯ является боковым ребром. Координаты его начала и конца равны: A(a/2; a/2; 0) и B(0; 0; h). Тогда координаты самого вектора:

Мы нашли все необходимые уравнения и вектора. Теперь остается воспользоваться рассмотренными формулами.

Рассчитаем сначала в пирамиде угол между плоскостями основания и боковой стороны. Соответствующие нормальные вектора равны: n 1 ¯(0; 0; 1) и n 2 ¯(0; 2*h; a). Тогда угол составит:

α = arccos(a / √(4 * h 2 + a 2))

Угол между плоскостью и ребром AB будет равен:

β = arcsin(h / √(a 2 / 2 + h 2))

Остается подставить конкретные значения стороны основания a и высоты h, чтобы получить необходимые углы.

Мерой угла между плоскостями является острый угол, образованный двумя прямыми, лежащими в этих плоскостях и проведенными перпендикулярно линии их пересечения.

Алгоритм построения

1. Из произвольной точки K проводят перпендикуляры к каждой из заданных плоскостей.
2. Способом вращения вокруг линии уровня определяют величину угла γ° с вершиной в точке K.
3. Вычисляют угол между плоскостями ϕ° = 180 – γ° при условии, что γ° > 90°. Если γ° < 90°, то ∠ϕ° = ∠γ°.

На рисунке представлен случай, когда плоскости α и β заданы следами. Все необходимые построения выполнены согласно алгоритму и описаны ниже.

Решение

1. В произвольном месте чертежа отмечаем точку K. Из неё опускаем перпендикуляры m и n соответственно к плоскостям α и β. Направление проекций m и n следующее: m""⊥f 0α , m"⊥h 0α , n""⊥f 0β , n"⊥h 0β .
2. Определяем действительный размер ∠γ° между прямыми m и n. Для этого вокруг фронтали f поворачиваем плоскость угла с вершиной K в положение, параллельное фронтальной плоскости проекции. Радиус поворота R точки K равен величине гипотенузы прямоугольного треугольника O""K""K 0 , катет которого K""K 0 = y K – y O .
3. Искомый угол ϕ° = ∠γ°, поскольку ∠γ° острый.

На рисунке ниже показано решение задачи, в которой требуется найти угол γ° между плоскостями α и β, заданными параллельными и пересекающимися прямыми соответственно.

Решение

1. Определяем направление проекций горизонталей h 1 , h 2 и фронталей f 1 , f 2 , принадлежащих плоскостям α и β, в порядке, указанном стрелками. Из произвольной точки K на пл. α и β опускаем перпендикуляры e и k. При этом e""⊥f"" 1 , e"⊥h" 1 и k""⊥f"" 2 , k"⊥h" 2 .
2. Определяем ∠γ° между прямыми e и k. Для этого проводим горизонталь h 3 и вокруг неё поворачиваем точку K в положение K 1 , при котором △CKD станет параллелен горизонтальной плоскости и отразится на ней в натуральную величину – △C"K" 1 D". Проекция центра поворота O" находится на проведенном к h" 3 перпендикуляре K"O". Радиус R определяется из прямоугольного треугольника O"K"K 0 , у которого сторона K"K 0 = Z O – Z K .
3. Значение искомого ∠ϕ° = ∠γ°, так как угол γ° острый.

Статья рассказывает о нахождении угла между плоскостями. После приведения определения зададим графическую иллюстрацию, рассмотрим подробный способ нахождения методом координат. Получим формулу для пересекающихся плоскостей, в которую входят координаты нормальных векторов.

Yandex.RTB R-A-339285-1

В материале будут использованы данные и понятия, которые ранее были изучены в статьях про плоскость и прямую в пространстве. Для начала необходимо перейти к рассуждениям, позволяющим иметь определенный подход к определению угла между двумя пересекающимися плоскостями.

Заданы две пересекающиеся плоскости γ 1 и γ 2 . Их пересечение примет обозначение c . Построение плоскости χ связано с пересечением этих плоскостей. Плоскость χ проходит через точку М в качестве прямой c . Будет производиться пересечение плоскостей γ 1 и γ 2 с помощью плоскости χ . Принимаем обозначения прямой, пересекающей γ 1 и χ за прямую a , а пересекающую γ 2 и χ за прямую b . Получаем, что пересечение прямых a и b дает точку M .

Расположение точки M не влияет на угол между пересекающимися прямыми a и b , а точка M располагается на прямой c , через которую проходит плоскость χ .

Необходимо построить плоскость χ 1 с перпендикулярностью к прямой c и отличную от плоскости χ . Пересечение плоскостей γ 1 и γ 2 с помощью χ 1 примет обозначение прямых а 1 и b 1 .

Видно, что при построении χ и χ 1 прямые a и b перпендикулярны прямой c , тогда и а 1 , b 1 располагаются перпендикулярно прямой c . Нахождение прямых a и а 1 в плоскости γ 1 с перпендикулярностью к прямой c , тогда их можно считать параллельными. Таки же образом расположение b и b 1 в плоскости γ 2 с перпендикулярностью прямой c говорит об их параллельности. Значит, необходимо сделать параллельный перенос плоскости χ 1 на χ , где получим две совпадающие прямые a и а 1 , b и b 1 . Получаем, что угол между пересекающимися прямыми a и b 1 равен углу пересекающихся прямых a и b .

Рассмотрим не рисунке, приведенном ниже.

Данное суждение доказывается тем, что между пересекающимися прямыми a и b имеется угол, который не зависит от расположения точки M , то есть точки пересечения. Эти прямые располагаются в плоскостях γ 1 и γ 2 . Фактически, получившийся угол можно считать углом между двумя пересекающимися плоскостями.

Перейдем к определению угла между имеющимися пересекающимися плоскостями γ 1 и γ 2 .

Определение 1

Углом между двумя пересекающимися плоскостями γ 1 и γ 2 называют угол, образовавшийся путем пересечения прямых a и b , где плоскости γ 1 и γ 2 имеют пересечение с плоскостью χ , перпендикулярной прямой c .

Рассмотрим рисунок, приведенный ниже.

Определение может быть подано в другой форме. При пересечении плоскостей γ 1 и γ 2 , где c – прямая, на которой они пересеклись, отметить точку M , через которую провести прямые a и b , перпендикулярные прямой c и лежащие в плоскостях γ 1 и γ 2 , тогда угол между прямыми a и b будет являться углом между плоскостями. Практически это применимо для построения угла между плоскостями.

При пересечении образуется угол, который по значению меньше 90 градусов, то есть градусная мера угла действительна на промежутке такого вида (0 , 90 ] . Одновременно данные плоскости называют перпендикулярнымив случае, если при пересечении образуется прямой угол. Угол между параллельными плоскостями считается равным нулю.

Обычный способ для нахождения угла между пересекающимися плоскостями – это выполнение дополнительных построений. Это способствует определять его с точностью, причем делать это можно с помощью признаков равенства или подобия треугольника, синусов, косинусов угла.

Рассмотрим решение задач на примере из задач ЕГЭ блока C 2 .

Пример 1

Задан прямоугольный параллелепипед А В С D A 1 B 1 C 1 D 1 , где сторона А В = 2 , A D = 3 , А А 1 = 7 , точка E разделяет сторону А А 1 в отношении 4: 3 . Найти угол между плоскостями А В С и В E D 1 .

Решение

Для наглядности необходимо выполнить чертеж. Получим, что

Наглядное представление необходимо для того, чтобы было удобней работать с углом между плоскостями.

Производим определение прямой линии, по которой происходит пересечение плоскостей А В С и В E D 1 . Точка B является общей точкой. Следует найти еще одну общую точку пересечения. Рассмотрим прямые D A и D 1 E , которые располагаются в одной плоскости A D D 1 . Их расположение не говорит о параллельности, значит, они имеют общую точку пересечения.

Однако, прямая D A расположена в плоскости А В С, а D 1 E в B E D 1 . Отсюда получаем, что прямые D A и D 1 E имеют общую точку пересечения, которая является общей и для плоскостей А В С и B E D 1 . Обозначает точку пересечения прямых D A и D 1 E буквой F . Отсюда получаем, что B F является прямой, по которой пересекаются плоскости А В С и В E D 1 .

Рассмотрим на рисунке, приведенном ниже.

Для получения ответа необходимо произвести построение прямых, расположенных в плоскостях А В С и В E D 1 с прохождением через точку, находящуюся на прямой B F и перпендикулярной ей. Тогда получившийся угол между этими прямыми считается искомым углом между плоскостями А В С и В E D 1 .

Отсюда видно, что точка A – проекция точки E на плоскость А В С. Необходимо провести прямую, пересекающую под прямым углом прямую B F в точке М. Видно, что прямая А М – проекция прямой Е М на плоскость А В С, исходя из теоремы о тех перпендикулярах A M ⊥ B F . Рассмотрим рисунок, изображенный ниже.

∠ A M E - это искомый угол, образованный плоскостями А В С и В E D 1 . Из получившегося треугольника А Е М можем найти синус, косинус или тангенс угла, после чего и сам угол, только при известных двух сторонах его. По условию имеем, что длина А Е находится таким образом: прямая А А 1 разделена точкой E в отношении 4: 3 , то означает полную длину прямой – 7 частей, тогда А Е = 4 частям. Находим А М.

Необходимо рассмотреть прямоугольный треугольник А В F . Имеем прямой угол A с высотой А М. Из условия А В = 2 , тогда можем найти длину A F по подобию треугольников D D 1 F и A E F . Получаем, что A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4

Необходимо найти длину стороны B F из треугольника A B F , используя теорему Пифагора. Получаем, что B F   = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Длина стороны А М находится через площадь треугольника A B F . Имеем, что площадь может равняться как S A B C = 1 2 · A B · A F , так и S A B C = 1 2 · B F · A M .

Получаем, что A M = A B · A F B F = 2 · 4 2 5 = 4 5 5

Тогда можем найти значение тангенса угла треугольника А Е М. Получим:

t g ∠ A M E = A E A M = 4 4 5 5 = 5

Искомый угол, получаемый пересечением плоскостей А В С и B E D 1 равняется a r c t g 5 , тогда при упрощении получим a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Ответ: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .

Некоторые случаи нахождения угла между пересекающимися прямыми задаются при помощи координатной плоскости О х у z и методом координат. Рассмотрим подробней.

Если дана задача, где необходимо найти угол между пересекающимися плоскостями γ 1 и γ 2 , искомый угол обозначим за α .

Тогда заданная система координат показывает, что имеем координаты нормальных векторов пересекающихся плоскостей γ 1 и γ 2 . Тогда обозначим, что n 1 → = n 1 x , n 1 y , n 1 z является нормальным вектором плоскости γ 1 , а n 2 → = (n 2 x , n 2 y , n 2 z) - для плоскости γ 2 . Рассмотрим подробное нахождение угла, расположенного между этими плоскостями по координатам векторов.

Необходимо обозначить прямую, по которой происходит пересечение плоскостей γ 1 и γ 2 буквой c . На прямой с имеем точку M , через которую проводим плоскость χ , перпендикулярную c . Плоскость χ по прямым a и b производит пересечение плоскостей γ 1 и γ 2 в точке M . из определения следует, что угол между пересекающимися плоскостями γ 1 и γ 2 равен углу пересекающихся прямых a и b , принадлежащих этим плоскостям соответственно.

В плоскости χ откладываем от точки M нормальные векторы и обозначаем их n 1 → и n 2 → . Вектор n 1 → располагается на прямой, перпендикулярной прямой a , а вектор n 2 → на прямой, перпендикулярной прямой b . Отсюда получаем, что заданная плоскость χ имеет нормальный вектор прямой a , равный n 1 → и для прямой b , равный n 2 → . Рассмотрим рисунок, приведенный ниже.

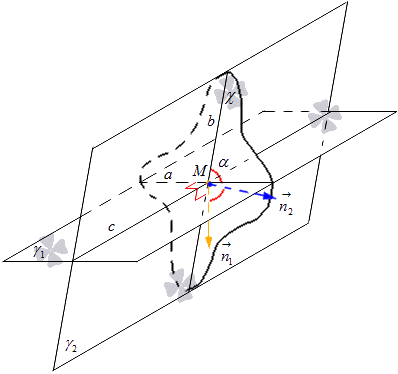
Отсюда получаем формулу, по которой можем вычислить синус угла пересекающихся прямых при помощи координат векторов. Получили, что косинусом угла между прямыми a и b то же, что и косинус между пересекающимися плоскостями γ 1 и γ 2 выводится из формулы cos α = cos n 1 → , n 2 → ^ = n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2 , где имеем, что n 1 → = (n 1 x , n 1 y , n 1 z) и n 2 → = (n 2 x , n 2 y , n 2 z) являются координатами векторов представленных плоскостей.

Вычисление угла между пересекающимися прямыми производится по формуле

α = a r c cos n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2

Пример 2

По условию дан параллелепипед А В С D A 1 B 1 C 1 D 1 , где А В = 2 , A D = 3 , А А 1 = 7 , а точка E разделяет сторону А А 1 4: 3 . Найти угол между плоскостями А В С и B E D 1 .

Решение

Из условия видно, что стороны его попарно перпендикулярны. Это значит, что необходимо ввести систему координат О х у z с вершиной в точке С и координатными осями О х, О у, О z . Необходимо поставить направление по соответствующим сторонам. Рассмотрим рисунок, приведенный ниже.

Пересекающиеся плоскости А В С и B E D 1 образуют угол, который можно найти по формуле α = a r c cos n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2 , в которой n 1 → = (n 1 x , n 1 y , n 1 z) и n 2 → = (n 2 x , n 2 y , n 2 z) являются нормальными векторами этих плоскостей. Необходимо определить координаты. По рисунку видим, что координатная ось О х у совпадает в плоскостью А В С, это значит, что координаты нормального вектора k → равняются значению n 1 → = k → = (0 , 0 , 1) .

За нормальный вектор плоскости B E D 1 принимается векторное произведение B E → и B D 1 → , где их координаты находятся путем координат крайних точек В, Е, D 1 , которые определяются, исходя из условия задачи.

Получаем, что B (0 , 3 , 0) , D 1 (2 , 0 , 7) . Потому как A E E A 1 = 4 3 , из координат точек A 2 , 3 , 0 , A 1 2 , 3 , 7 найдем E 2 , 3 , 4 . Получаем, что B E → = (2 , 0 , 4) , B D 1 → = 2 , - 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 - 3 7 = 12 · i → - 6 · j → - 6 · k → ⇔ n 2 → = (12 , - 6 , - 6)

Необходимо произвести подстановку найденных координат в формулу вычисления угла через арккосинус. Получаем

α = a r c cos 0 · 12 + 0 · (- 6) + 1 · (- 6) 0 2 + 0 2 + 1 2 · 12 2 + (- 6) 2 + (- 6) 2 = a r c cos 6 6 6 = a r c cos 6 6

Метод координат дает аналогичный результат.

Ответ: a r c cos 6 6 .

Завершающая задача рассматривается с целью нахождения угла между пересекающимися плоскостями при имеющихся известных уравнениях плоскостей.

Пример 3

Вычислить синус, косинус угла и значение угла, образованного двумя пересекающимися прямыми, которые определены в системе координат О х у z и заданы уравнениями 2 x - 4 y + z + 1 = 0 и 3 y - z - 1 = 0 .

Решение

При изучении темы общего уравнения прямой вида A x + B y + C z + D = 0 выявили, что А, В, С являются коэффициентами, равными координатам нормального вектора. Значит, n 1 → = 2 , - 4 , 1 и n 2 → = 0 , 3 , - 1 являются нормальным векторами заданных прямых.

Необходимо подставить координаты нормальных векторов плоскостей в формулу вычисления искомого угла пересекающихся плоскостей. Тогда получаем, что

α = a r c cos 2 · 0 + - 4 · 3 + 1 · (- 1) 2 2 + - 4 2 + 1 2 = a r c cos 13 210

Отсюда имеем, что косинус угла принимает вид cos α = 13 210 . Тогда угол пересекающихся прямых не является тупым. Подставив в тригонометрическое тождество, получаем, что значение синуса угла равняется выражению. Вычислим и получим, что

sin α = 1 - cos 2 α = 1 - 13 210 = 41 210

Ответ: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter